Tensors
Un tensore è un'array n-dimensionale di numeri scalari.
Un tensore ad una dimensione è anche detto vettore. (rank 1)
Un tensore a due dimensioni è anche detto matrix. (rank 2)
Il rank è il numero di assi (o dimensioni) del tensore. Uno scalare ha rank 0.
Lo shape è la dimensione di ogni asse del tensore.
# a scalar number 23, shape = []
torch.tensor(23.0)
# a vector with one number in it, shape = [1]
torch.tensor([23.0])
# a vector with more numbers in it, shape = [3]
torch.tensor([23.0, 12.0, 34.0])
# a matrix 2 x 3, shape = [2, 3]
torch.tensor([ [2,3,4], [4,5,6]])
# a 3 dimensions tensor, shape = [2, 2, 3]
# contains 2 rows,
# each rpw has 2 arrays,
# and every array has 3 elements
torch.tensor([
[ [2,3,4], [4,5,6] ],
[ [7,8,9], [10, 12, 13] ]
])
funzioni di base utili
t = torch.tensor([
[ [2,3,4], [4,5,6] ],
[ [7,8,9], [10, 12, 13] ],
[ [14, 15 18], [14, 22, 23] ]
])
# numero di elementi totali di un tensore
t.numel() # 18
# forma del tensore
t.shape # torch.Size([3, 2, 3])
# crea un tensore di zeri di 2 righe e 3 colonne
torch.zeros([2,3])
#tensor([[0., 0., 0.],
# [0., 0., 0.]])
# crea un tensore di uno di 2 righe e 3 colonne
torch.ones([2,3])
#tensor([[1., 1., 1.],
# [1., 1., 1.]])
# crea un tensore in range [0,7]
torch.arange(7, dtype=torch.int32)
# tensor([0, 1, 2, 3, 4, 5, 6], dtype=torch.int32)
# view, cambia la vista del tensore,
# nota che il prodotto delle nuove dimensioni DEVE ESSERE LO STESSO del
# prodotto delle vecchie dimensioni.
t = tensor([[[ 2, 3, 4],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 12, 13]],
[[14, 15, 18],
[14, 22, 23]]])
# t shape = [3, 2, 3]
t.view(3,6)
tensor([[ 2, 3, 4, 4, 5, 6],
[ 7, 8, 9, 10, 12, 13],
[14, 15, 18, 14, 22, 23]])
t.view(6, 3)
tensor([[ 2, 3, 4],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 12, 13],
[14, 15, 18],
[14, 22, 23]])
t.view(18)
tensor([ 2, 3, 4, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, 18, 14, 22, 23])
indici
t = torch.tensor([
[[ 2, 3, 4],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 12, 13]],
[[14, 15, 18],
[14, 22, 23]]])
# prima riga
t[0]
tensor([[2, 3, 4],
[4, 5, 6]])
# secondo array della prima riga
t[0,1]
tensor([4, 5, 6])
# terzo elemento del secondo array della prima riga
t[0,1,2]
tensor(6)
# Slicing:
# accedi alla prima e seconda riga
t[:2]
tensor([[[ 2, 3, 4],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 12, 13]]])
# tutti gli elementi della seconda colonna degli array dentro la prima riga
t[0, :, 1]
tensor([ 3, 5])
t1 = torch.arange(10)
tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
#accedi a tutti gli elementi meno l'ultimo
t1[:-1]
tensor([0, 1, 2, 3, 4, 5, 6, 7, 8])
Operazioni
t = torch.tensor([
[
[1, 2],
[3, 4]
],
[
[5, 6],
[7, 8]
]
])
t.shape
# 2 righe, ogni riga ha 2 array da 2 colonne
torch.Size([2, 2, 2])
t.sum()
tensor(36)
# somma scegliendo la dimensione da ridurre
# somma primo elemento della prima riga con primo elemento della seconda riga (dim 0)
# 6 = 1 + 5
# 6 = t[0,0,0] + t[1,0,0]
t.sum(dim=0)
tensor([[ 6, 8],
[10, 12]])
# mantenendo la dimensionalità:
t.sum(dim=0, keepdim=True)
tensor([[[ 6, 8],
[10, 12]]])
t.sum(dim=0, keepdim=True).shape
torch.Size([1, 2, 2])
# somma per le colonne degli array interni (dim 1)
# 4 = 1 + 3
# 4 = t [0,0,0] + t[0, 1, 0]
t.sum(dim=1)
tensor([[ 4, 6],
[12, 14]])
# mantenendo la dimensionalità:
t.sum(dim=1, keepdim=True)
tensor([[[ 4, 6]],
[[12, 14]]])
t.sum(dim=1, keepdim=True).shape
torch.Size([2, 1, 2])
# somma per le righe degli array interni (dim 2)
# 3 = 1 + 2
# 3 = t [0,0,0] + t[0, 0, 1]
t.sum(dim=2)
tensor([[ 3, 7],
[11, 15]])
# mantenendo la dimensionalità:
t.sum(dim=2, keepdim=True)
tensor([[[ 3],
[ 7]],
[[11],
[15]]])
t.sum(dim=2, keepdim=True).shape
torch.Size([2, 2, 1])
Moltiplicazione tra matrici a @ b
Vengono moltiplicati gli elementi della riga del primo tensore per l'elemento corrispondente della colonna del secondo tensore. Poi i prodotti vengono sommati tra di loro.
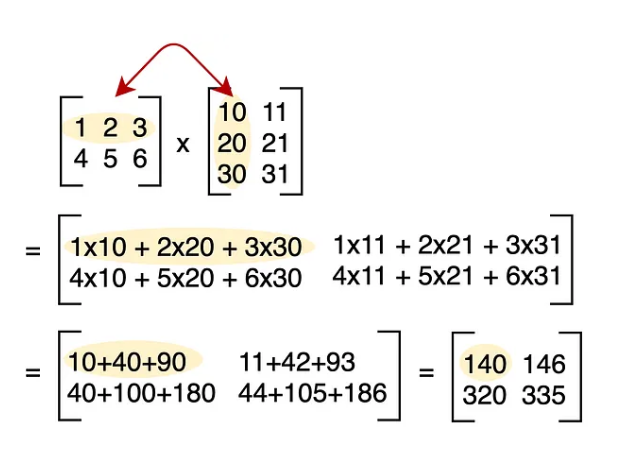
Per effettuare la moltiplicazione tra 2 tensori è fondamentale che
l'ultima dimensione del primo tensore sia uguale alla prima dimensione del secondo tensore!
esempio:
a = torch.tensor([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
# a.shape: [3, 3]
b = torch.tensor([[0, 4],
[0, 3],
[8, 4]])
# b.shape = [3, 2]
c = a @ b
# c.shape = [3, 2]
# c = [16, 11],
# [40, 44],
# [64, 77]
# dove:
# 16 = (0*0) + (1*0) + (2*8)
# 11 = (0*4) + (1*3) + (2*4)
# 40 = (3*0) + (4*0) + (5*8)
# 44 = (3*4) + (4*3) + (5*4)
# etc etc
Si noti che la moltiplicazione di matrice ha l'effetto di lasciare intatte le dimensioni del primo tensore, tranne l'ultima:
torch.randn(4, 80) @ torch.randn(80, 200) = torch.Size([4, 200])
torch.randn(4, 5, 80) @ torch.randn(80, 200) = torch.Size([4, 5, 200])
torch.randn(4, 5, 3, 80) @ torch.randn(80, 200) = torch.Size([4, 5, 3, 200])
torch.randn(4, 5, 3, 6, 80) @ torch.randn(80, 200) = torch.Size([4, 5, 3, 6, 200])
Esiste un bel sito che spiega graficamente come viene fatta la moltiplicazione tra matrici: http://matrixmultiplication.xyz/
Softmax di una matrice
Questa operazione viene usata per normalizzare i valori di una matrice.
Viene prima calcolato l'exp() di ogni elemento della matrice e poi viene effettuata
la divisione per la somma della riga di tale matrice.
Eseguire l'esponenziale sugli elementi di un tensore serve per eliminarne i valori negativi, trasformandoli in positivi.
Effettuare la divisione per la somma di riga ha effetto di normalizzare i valori della matrice,
difatti la somma degli elementi di riga dopo aver applicato softmax() risulta pari a 1.
# softmax:
# 1) exp...
p = p.exp()
# 2) normalizzare
p = p / p.sum()
# oppure in pytorch:
p = F.softmax(p, dim=-1) # con somma effettuata sull'ultima dimensione