WaveNet, a convolutional NN

Vogliamo creare una rete che, come visto finora, determina il prossimo carattere sulla base di un contesto di block_size caratteri precedenti.
Useremo un tipo di rete (deepmind wavenet) in cui vengono fusi i due elementi adiacenti dei suoi hidden layer.
L'insieme dei due elementi adiacenti concorre alla scelta del prossimo carattere che farà parte del layer successivo.

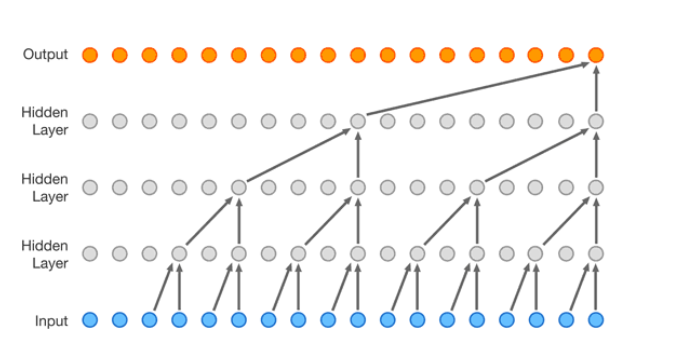
wavenet1

La convoluzione ha l'effetto simile a quello di un ciclo for, usato per determinare in parallelo gli output (pallini arancio). Ogni hidden layer di una rete convoluzionale è una sorta di filtro che facciamo scorrere lungo la sequenza dei dati in input.

Partendo dal solito boilerplate iniziale, abbiamo già ricavato i set di dati di input:
consideriamo block_size = 8.

Xtr,  Ytr  = build_dataset(words[:n1])     # training set (80% of total)
Xdev, Ydev = build_dataset(words[n1:n2])   # validation set (10% of total)
Xte,  Yte  = build_dataset(words[n2:])     # test set (10% of total)

# shapes:
# Xtr:  torch.Size([182625, 8]), Ytr:  torch.Size([182625])
# Xdev: torch.Size([22655, 8]),  Ydev: torch.Size([22655])
# Xte:  torch.Size([22866, 8]),  Yte:  torch.Size([22866])

Consideriamo un subset di 4 dati a caso che daremo in input alla rete:

ix = torch.randint(0, Xtr.shape[0], (4,)) # estraggo 4 numeri a caso tra 0 e dim massima di Xtr (182625)
Xb, Yb = Xtr[ix], Ytr[ix]
# Xb.shape: [4, 8], Xb: tensor([[ 0,  0,  0,  0, 26,  1, 18,  9],
#                               [ 0,  0,  5, 12, 19, 16,  5, 20],
#                               [ 0,  0,  0,  0,  0,  0, 12,  5],
#                               [ 0,  0, 12, 15, 18,  1, 12, 25]])
# Yb.shape: [4], Yb: tensor([12, 20,  1, 20])

Vogliamo accorpare i caratteri adiacenti degli input in questo modo:

[ 0,  0,  0,  0, 26,  1, 18,  9] => [ (0,  0),  (0,  0), (26,  1), (18,  9)]

per poi poterli elaborare in parallelo.
Per implementare tutto ciò, partiamo dalla rete NN sviluppata prima.
In quella rete, considerando il subset di 4 dati, abbiamo in input:

X @ W + b
(torch.randn(4, 80) @ torch.randn(80, 200) + torch.randn(200)).shape # [4, 200]

Difatti entrano 80 caratteri in input ( i vettori 10-dimensionali accodati dal layer Flatten)
Se però accorpiamo i caratteri, in input avremo una forma [4, 4, 20], (4 gruppi di 2 caratteri, ogni gruppo è un vettore 10-dimensionale) e per rispettare la moltiplicazione @ tra matrici avremo:

X @ W + b
(torch.randn(4, 4, 20) @ torch.randn(20, 200) + torch.randn(200)).shape # [4, 4, 200]

Flatten Consecutive

Perciò va modificato il layer Flatten, per fare in modo che restituisca 4 gruppi di 2 caratteri tra loro adiacenti.

# partendo da: 
l = list(range(10)) # [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

# se volessi prendere gli elementi di indice pari (estrai a 2 a 2 partendo da indice 0):
l[::2] # [0, 2, 4, 6, 8]

# mentre, quelli di indice dispari ( estrai a 2 a 2 partendo da indice 1):
l[1::2] # [1, 3, 5, 7, 9]

# sui nostri dati di input:
explicit = torch.cat([e[:, ::2, :], e[:, 1::2, :]], dim=2) # shape = [4, 4, 20]

# che equivale a scrivere:
e.view(4, 4, 20)

# difatti sono equivalenti:
(e.view(4, 4, 20) == explicit).all() # tensor(True)

Generalizzando possiamo quindi usare pytorch view() per adattare il tensore di input alla nuova forma.
Usando n variabile possiamo creare varie forme.
Nel nostro caso n = 2.

class FlattenConsecutive:
  
  def __init__(self, n):
    self.n = n
    
  def __call__(self, x):
    B, T, C = x.shape
    x = x.view(B, T//self.n, C*self.n)
    if x.shape[1] == 1:
      x = x.squeeze(1)
    self.out = x
    return self.out

  def parameters(self):
    return []

Implementazione:

n_embd = 10 # the dimensionality of the character embedding vectors
n_hidden = 200 # the number of neurons in the hidden layer of the MLP

model = Sequential([
  Embedding(vocab_size, n_embd), 
  FlattenConsecutive(2), Linear(n_embd * 2, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(), # nota la dimensione Linear fan_in = 20 
                                                                                                  # per moltiplicare correttamente con l'output di 
                                                                                                  # FlattenConsecutive (4, 4, 20)
  FlattenConsecutive(2), Linear(n_hidden * 2, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(), # nota la dimensione Linear fan_in= 400 
                                                                                                  # per moltiplicare correttamente con l'output di
                                                                                                  # FlattenConsecutive (4, 2, 400) 
  FlattenConsecutive(2), Linear(n_hidden * 2, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(), # idem come per il layer precedente
  Linear(n_hidden, vocab_size),
])
# ...
#eseguendo poi il tutto con 
logits = model(Xb)

avremo le forme dei layer:

for layer in model.layers:
  print(layer.__class__.__name__, ':', tuple(layer.out.shape))

# Embedding : (4, 8, 10)
# FlattenConsecutive : (4, 4, 20)  <--------
# Linear : (4, 4, 200)
# BatchNorm1d : (4, 4, 200)
# Tanh : (4, 4, 200)
# FlattenConsecutive : (4, 2, 400) <-------
# Linear : (4, 2, 200)
# BatchNorm1d : (4, 2, 200)
# Tanh : (4, 2, 200)
# FlattenConsecutive : (4, 400) <--------
# Linear : (4, 200)
# BatchNorm1d : (4, 200)
# Tanh : (4, 200)
# Linear : (4, 27)

Nota che l'effetto di FlattenConsecutive, per n=2, è quello di togliere 2 dimensioni ad ogni passaggio.

AI appunti

WaveNet, a convolutional NN

Flatten Consecutive