MakeMore, a classifier neural network

Vogliamo creare una rete con 3 layer:

input layer
hidden layer
output layer

Per la definizione di rete neurale, i neuroni dello stesso layer non comunicano tra di loro.
Ogni neurone è completamente connesso al neurone del layer successivo, per cui l'uscita di un neurone vanno in ingresso di tutti i neuroni del layer successivo.

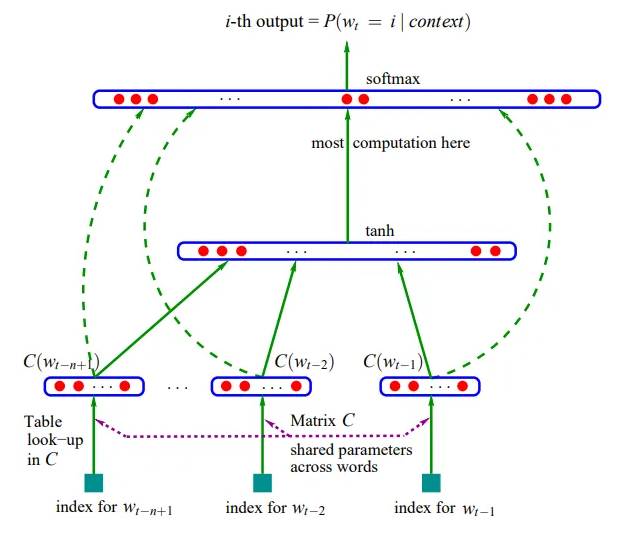
Neural Network

Pensando di voler implementare le rete makemore, 27 caratteri dell'alfabeto codificati in lookup table (embeddings), rete che accetta sequenze di 3 caratteri in input per produrre un quarto carattere in output, possiamo procedere così:

Input layer

Avremo 27 neuroni, ognuno ha un input che accetta uno tra i 27 caratteri dell'alfabeto.

# input, sequenze di 3 caratteri, immaginiamo di avere 32 input..
X = [
    [5, 13, 13],
    [13, 13, 1],
    [...],
    ...,
    ,,,
]
# X.shape = [32, 3]

# Input layer 
emb = C[X]
# emb.shape =  torch.Size([32, 3, 2])
# emb contiene 32 righe, ogni riga ha 3 elementi, cioè 3 array,
# ogni array contiene due numeri, cioè la codifica di un carattere nello spazio a 2 dinensioni (carattere embeddato)

Possiamo considerare emb come il nostro input layer:
ci sono 27 neuroni, ognuno accetta in ingresso 1 carattere,
C è la matrix dei pesi.

Hidden layer

Avremo un numero di neuroni prefissato in progetto, es.: 100.
ogni neurone accetta in input tutti gli output dei neuroni dell'input layer, che sono: emb.shape = torch.Size([32, 3, 2]) -> "tre volte due" cioè 6 input.
Quindi creiamo i pesi e bias per i neuroni:

# 6 righe (input), ogni riga contiene 1 array di 100 numeri (pesi), uno per ogni neurone
W1 = torch.randn([6, 100])

# 100 bias, uno per ogni neurone
b1 = torch.randn(100)

# output dell'hidden layer
# Y1 = W1 @ emb + b1

# N.B.:  W1 @ emb --> ERRORE! --> shapes cannot be multiplied (96x2 and 6x100)
# forme dei tensori non compatibili!!
# cambiamo forma emb:
emb.view(32, 6) 

h = emb.view(32, 6) @ W1 + b1
# h shape = torch.Size([32, 100])

# supponiamo anche che esista una funzione di attivazione tanh
h = torch.tanh(emb.view(32, 6) @ W1 + b1) 
# h shape = torch.Size([32, 100])

# h rappresenta le attivazioni dei 100 neuroni

Output layer

Avremo 27 neuroni nel layer, perché possiamo avere uno tra 27 caratteri, come quarto carattere da prevedere nella sequenza.
Ha 100 input ( gli output dei neuroni dell'hidden layer)
Ed ha 27 output

# 100 input, 27 output
# avremo 100 righe, ogni riga contiene un array di 27 pesi.
W2 = torch.randn([100, 27])
b2 = torch.randn(27)

logits = h @ W2 + b2
# logits shape =  torch.Size([32, 27])
# la forma

la forma dei logits è ok perché per 32 righe (le 32 stringhe in input), avremo 27 possibili output

Calcolo dell'output della rete (forward pass)

# forward pass
  emb = C[X] # (32,6)
  h = torch.tanh(emb.view(32, 6) @ W1 + b1) # (32, 100)
  logits = h @ W2 + b2 # (32, 27)
  loss = F.cross_entropy(logits, Y)

Backpropagation della rete (backward pass)

Agendo su tutti i parametri della rete, impostiamo i gradienti.

parameters = [C, W1, b1, W2, b2]
for p in parameters: # dotiamoli di gradiente
    p.requires_grad = True

iterando per epoch n volte effettuiamo il passaggio in avanti,
poi calcoliamo tutti i gradienti
e quindi aggiorniamo i valori dei parametri, applicando un certo learning rate.

epoch = 100
learning_rate = -0.1

for _ in range(epoch): # epoch
    for p in parameters: # safety: inizializzare tutti i gradienti a None 0 a zero.
        p.grad = None

    # 1) forward pass
    emb = C[X] # (32,6)
    h = torch.tanh(emb.view(32, 6) @ W1 + b1) # (32, 100)
    logits = h @ W2 + b2 # (32, 27)
    loss = F.cross_entropy(logits, Y)
    
    # 2) backward pass, calcoliamo tutti i gradienti
    print ('loss=', loss.item())

    loss.backward()

    # 3) update dei parametri
    for p in parameters:
        p.data += -learning_rate * p.grad

AI appunti