Implementing Backpropagation
Staged computation example
Introdurremo un calcolo a fasi (staged computation) della backpropagation di una funzione.
Difatti è utile scomporre la funzione in equazioni semplici, aiutandosi anche attraverso variabili intermedie di appoggio,
per poter applicare la chain rule in modo semplice.
Esempio: Consideriamo la seguente funzione:
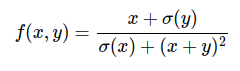
Vogliamo calcolarne i gradienti per gli input: x=3, y=-4.
proviamo a scomporla:
x = 3 # example values
y = -4
# forward pass
sigy = 1.0 / (1 + math.exp(-y)) # sigmoid in numerator #(1)
num = x + sigy # numerator #(2)
sigx = 1.0 / (1 + math.exp(-x)) # sigmoid in denominator #(3)
xpy = x + y #(4)
xpysqr = xpy**2 #(5)
den = sigx + xpysqr # denominator #(6)
invden = 1.0 / den #(7)
f = num * invden # done! #(8)
e ragionando a ritroso, proviamo a calcolarne i gradienti e applicando la chain rule:
# backprop f = num * invden #(8)
# derivate di semplice moltiplicazione
dnum = invden
dinvden = num
# backprop invden = 1.0 / den #(7)
# derivata di divisione = f'(x) 1/x = -1/x*2
# e poi applico moltiplicazione di chain rule
dden = (-1/(den**2)) * dinvden
# backprop den = sigx + xpysqr (denominator)
# derivata di addizione
dsigx = 1 * dden
dxpysqr = 1 * dden
# backprop xpysqr = xpy**2 #(5)
# derivata di elevazione a potenza x**2 = 2x
dxpy = (2 * xpy) * dxpysqr
# xpy = x + y #(4)
dx = 1 * dxpy
dy = 1 * dxpy
# sigx = 1.0 / (1 + math.exp(-x)) sigmoid in denominator #(3)
# x è coinvolta in 2 operazioni!,
# i gradienti vanno sommati!
dx += ((1 - sigx) * sigx) * dsigx
# num = x + sigy # numerator #(2)
dx+= 1.0 * dnum
dsygy = 1.0 * dnum
# sigy = 1.0 / (1 + math.exp(-y)) # sigmoid in numerator #(1)
dy += ((1 - sigy) * sigy) * dsigy