Learning Rate
Trovare un giusto valore del learning rate non è un'operazione banale.
Un learning rate troppo alto può accelerare il training, ma il modello può superare i minimi e funzionerà male.
Di contro, un learning rate troppo basso renderà il training eccessivamente lento e il modello può rimanere
bloccato in punti di minimo locali.
Immaginando, comunque, di aver scelto un valore del learning rate da usare, esso va applicato nell'algoritmo del backpropagation:
es.: partiamo dal seguente algoritmo di backward
epoch = 100
learning_rate = -0.001
for _ in range(epoch):
for p in parameters: # safety: inizializzare tutti i gradienti a None 0 a zero.
p.grad = None
# 1) forward pass
emb = C[X] # (32,6)
h = torch.tanh(emb.view(32, 6) @ W1 + b1) # (32, 100)
logits = h @ W2 + b2 # (32, 27)
loss = F.cross_entropy(logits, Y)
# 2) backward pass, calcoliamo tutti i gradienti
print ('loss=', loss.item())
loss.backward()
# 3) update dei parametri
for p in parameters:
p.data += -learning_rate * p.grad
Generalmente il learning rate viene passato in argomento ad un optimizer che provvederà ad applicarlo all'interno della backpropagation.
Learning rate variabile (Scheduler)
In genere usare un learning rate fisso è poco efficiente, dilata i tempi di training e non assicura una corretta discesa del gradiente.
E' stato sperimentato che usare learning rate variabili può risolvere questi problemi, ottimizzando i tempi di training e migliorando la discesa del gradiente, di fatto aumentando le prestazioni di training del modello.
Per questo in pytorch ci sono molti tipi di scheduler che adattano i valori del learning rate durante la discesa del gradiente (SGD) nel training loop.
Ricordando che durante il training loop viene usato un optimizer per aggiornare i pesi e che il learning rate è un parametro dell'optimizer, uno scheduler è un algoritmo che aggiorna il valore del learning rate all'interno dell'optimizer.
Es.:
import torch
import torch.optim as optim
import torch.optim.lr_scheduler as lr_scheduler
scheduler = lr_scheduler.LinearLR(optimizer, start_factor=1.0, end_factor=0.3, total_iters=10)
Nota che uno scheduler pytorch prende l'optimizer come primo parametro.
Esempio dell'andamento del valore del learning rate, gestito da uno scheduler:
model = torch.nn.Linear(2, 1)
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
scheduler = torch.optim.lr_scheduler.CyclicLR(optimizer, base_lr=0.001, max_lr=0.1,step_size_up=5,mode="triangular2")
lrs = []
for i in range(100):
optimizer.step()
lrs.append(optimizer.param_groups[0]["lr"])
# print("Factor = ",i," , Learning Rate = ",optimizer.param_groups[0]["lr"])
scheduler.step()
plt.plot(lrs)
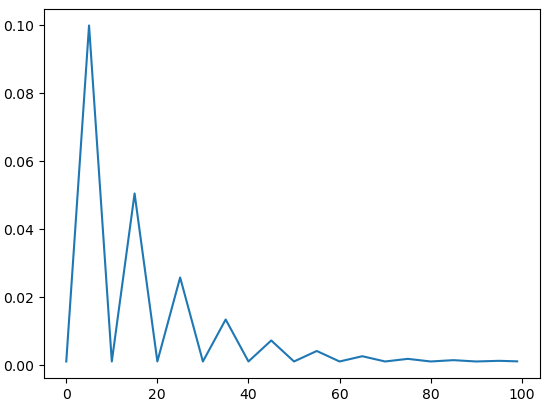
Aumento del learning rate
Immaginando di voler considerare learning_rate diversi nell'intervallo [0,0001, 1], possiamo creare tanti valori equidistanti tra loro in quell'intervallo:
# invece di fare direttamente:
learning_rates = torch.linspace(0.0001, 1, 1000)
# creiamo prima gli esponenti:
lre = torch.linspace(-1, 0, 1000)
learning_rates = 10**lre
# learning_rates = tensor([0.1000, 0.1002, 0.1005, 0.1007, 0.1009, 0.1012, 0.1014, 0.1016, ..., 1.0000])
Adesso applicando questi learning_rates all'algoritmo di backward faremo in modo che all'aumentare delle iterazioni per le epoch,
difatto verranno usati learning rates sempre più alti.
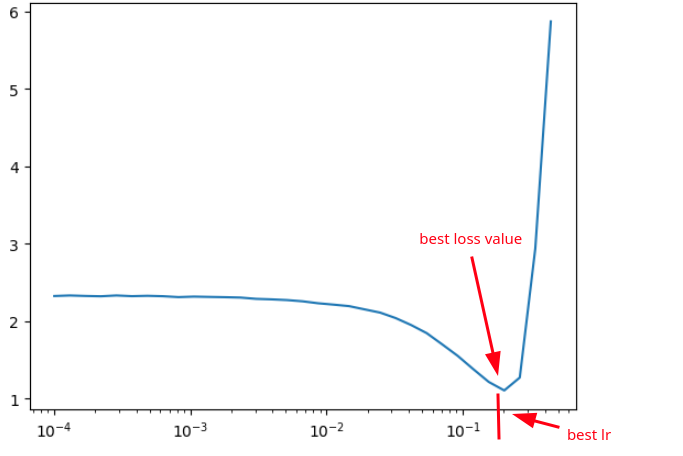
Plottando in istogramma con asse delle ascisse i valori del learning rate ed in ordinate il loss, si nota subito il miglior valore di learning rate da usare.
Da come si nota nel grafico, una volta raggiunto un ottimale valore del learning rate è ragionevole fermare il training del modello, visto che dopo inizia ad aumentare il valore del loss!
epoch = 10000
learning_rate = -0.001
lre_results = []
lr_results = []
loss_results = []
for i in range(epoch):
for p in parameters: # safety: inizializzare tutti i gradienti a None 0 a zero.
p.grad = None
# 1) forward pass
emb = C[X] # (32,6)
h = torch.tanh(emb.view(32, 6) @ W1 + b1) # (32, 100)
logits = h @ W2 + b2 # (32, 27)
loss = F.cross_entropy(logits, Y)
# 2) backward pass, calcoliamo tutti i gradienti
print ('loss=', loss.item())
loss.backward()
# 3) update dei parametri
lr = learning_rates[i]
for p in parameters:
p.data += -lr * p.grad
# track stats:
lr_results.append(lr)
lre_results.append(lre[i]) # memorizza l'esponente
loss_results.append(loss.item())
Possiamo graficare i risultati per vedere chiaramente come influiscono i vari valori del learning rate sulle perdite:
#plt(asse_x, asse_y)
plt(lr_results, loss_results)
Ma ancora più interessante è graficare l'array degli esponenti e i risultati delle perdite, perché mostra più chiaramente ancora la situazione e, quindi, la scelta di un corretto learning rate.
plt(lre_results, loss_results)
Quindi se dal grafico vediamo che un buon esponente è, ad esempio, -1, useremo come learning rate:
learning_rate = 10**-1 = 0.1
Decadimento del learning rate
E' possibile anche usare learning rates variabili in base alle iterazioni.
Esempio:
learning_rate = 0.1 if i < 100000 else 0.01 # step learning rate decay
Semplificazioni (lossi)
Per migliorare la visualizzazione in grafico, usiamo un'array lossi che contiene il log10 del valore del loss, per evidenziare meglio l'leffetto del learning rate durante il training.
esempio:
max_steps = 200000
batch_size = 32
lossi = []
for i in range(max_steps):
# minibatch construct
ix = torch.randint(0, Xtr.shape[0], (batch_size,))
Xb, Yb = Xtr[ix], Ytr[ix] # batch X,Y
# forward pass
logits = model(Xb)
loss = F.cross_entropy(logits, Yb) # loss function
# backward pass
for p in parameters:
p.grad = None
loss.backward()
# update: simple SGD
lr = 0.1 if i < 150000 else 0.01 # step learning rate decay
for p in parameters:
p.data += -lr * p.grad
# track stats
if i % 10000 == 0: # print every once in a while
print(f'{i:7d}/{max_steps:7d}: {loss.item():.4f}')
lossi.append(loss.log10().item())
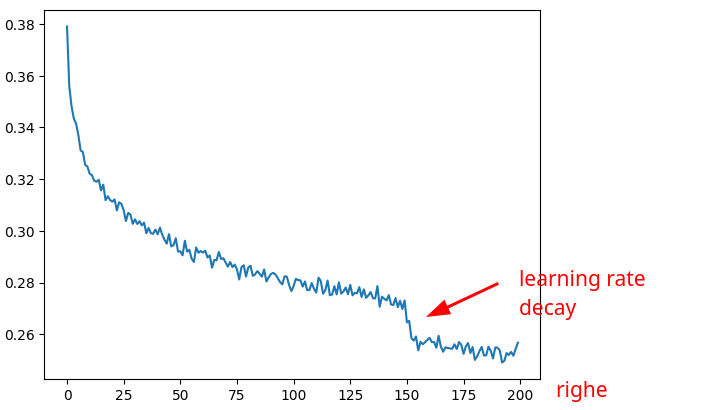
Per semplificare il grafico del loss, mettiamo lossi in un tensore e ne calcoliamo la media dei suoi valori ogni 1000 elementi.
t = torch.tensor(lossi) # shape = [200000]
# modifico la forma per ottenere n righe da 1000 elementi
t.view(-1, 1000) # shape = [200, 1000]
# calcolo la media
t.view(-1, 1000).mean(1)
# creo il grafico:
plt.plot(t.view(-1, 1000).mean(1))
che mostra chiaramente l'effetto del learning rate: